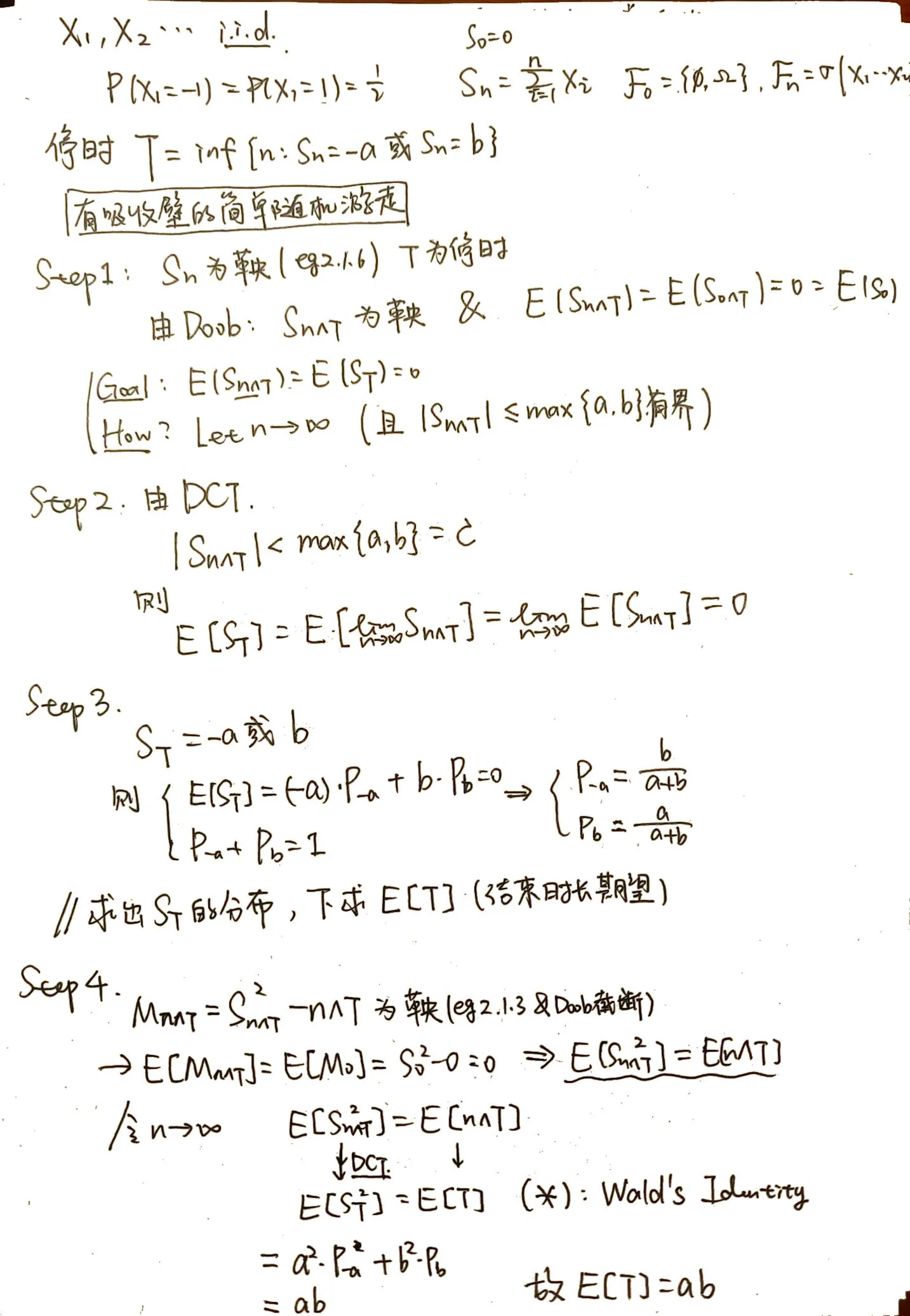前言
本报告整理了利用鞅理论和停时方法解决“一维随机游动”问题的解题过程要点,并初步探究了二维随机游动的相关问题。给出了包括有吸收壁的简单对称随机游走、单边游走与常返性、有偏的随机游走等三种典型情形的详细分析,讨论了吸收概率、期望停止时间等关键量的计算方法。
关键字:鞅,可选停止定理,吸收概率,期望停时,离散调和函数。
一维随机游走
Case I:有吸收壁的简单对称随机游走
设 X1,X2,… 独立同分布(i.i.d.),且 P(Xi=1)=P(Xi=−1)=1/2,随机游走过程定义为 S0=0,Sn=∑i=1nXi,Fn=σ(X1,…,Xn)。
定义停时 T=inf{n:Sn=−a 或 Sn=b},其中 a,b>0。
Step 1-3:计算吸收结果分布 P(ST=−a)、P(ST=b)
- 构造鞅: 过程 Sn 是一个鞅,因为 E[Sn∣Fn−1]=Sn−1+E[Xn]=Sn−1。
根据 Doob 可选停止定理,对于停时 T,过程 Sn∧T 也是一个鞅,因此 E[Sn∧T]=E[S0]=0。
- 控制收敛(DCT): 我们的目标是证明 E[ST]=0。
由于 Sn 在停时 T 之前始终位于 (−a,b) 区间内,所以 ∣Sn∧T∣≤max(a,b),即 Sn∧T 是一致有界的。
当 n→∞ 时,Sn∧T→ST。根据控制收敛定理,我们可以交换期望和极限:
E[ST]=E[limn→∞Sn∧T]=limn→∞E[Sn∧T]=0
- 吸收概率:在停时 T 刻,ST 的取值只能是 −a 或 b。设 Pa=P(ST=−a) 和 Pb=P(ST=b)。
{−aPa+bPb=0,Pa+Pb=1⇒⎩⎨⎧P(ST=−a)=a+bb,P(ST=b)=a+ba
Step 4:计算期望停止时间 E[T]
- 新的鞅:构造一个新过程 Mn=Sn2−n。这是一个鞅,因为:
E[Mn∣Fn−1]=E[Sn2−n∣Fn−1]=E[(Sn−1+Xn)2−n∣Fn−1]=E[Sn−12+2Sn−1Xn+Xn2−n∣Fn−1]=Sn−12+2Sn−1E[Xn]+E[Xn2]−n=Sn−12+0+1−n=(Sn−12−(n−1))=Mn−1
- 应用可选停止与收敛定理(OST):对鞅 Mn 应用可选停止定理,有 E[Mn∧T]=E[M0]=0,即 E[Sn∧T2]=E[n∧T]。
当 n→∞ 时,由于 Sn∧T2 有界,由 DCT 可得 E[Sn∧T2]→E[ST2]。
同时,由单调收敛定理 (MCT) 可得 E[n∧T]→E[T]。
因此,我们得到 E[ST2]=E[T],这即是 Wald′sIdentity 的一个特例。
- 求解 E[T]:
E[ST2]=(−a)2P(ST=−a)+b2P(ST=b)=a2a+bb+b2a+ba=a+bab(a+b)=ab
所以,期望停止时间为 E[T]=ab
Case II:单边停时与常返性
考虑一维对称随机游走是否会回到任意整数点(常返性)。
- 设停时 U=inf{n:Sn=−a},其中 a>0。我们想计算 P(U<∞)
- 我们可以借助双边吸收壁的结果。设另一个吸收壁在 b 处,停时为 Hb=inf{n:Sn=b}。总停时为 τ=U∧Hb
- 从 Case I 的结果可知,粒子被 b 吸收的概率为 P(Sτ=b)=a+ba
- 那么,不被 b 吸收(即被 −a 吸收)的概率为 P(Sτ=−a)=P(U<Hb)=a+bb
- b→∞,则 P(U<∞)=limb→∞a+bb=1
**结论:**一维对称随机游走是常返的,它终将到达任何一个整数点。
尝试求解 P(U=k)
方法一:组合计数
这种方法实际上就是在解决伯特兰选票问题(Bertrand’s Ballot Problem,1887).
我们的目标其实就是求解
P(T−a=k∣Sk=−a)=P(Sk=−a)P(T−a=k∩Sk=−a)=P(Sk=−a)P(T−a=k)=p0
即 “在已知第k步在-a被吸收的条件下,这是首次到达的概率”
定理:若 k 步中向右 m 步,则 P(T−a=k)=k∣a∣⋅2k(mk)。
下面介绍一下Bertrand选票问题中 p0的证明思路:
在一场选举中候选人A得到了p张选票,而候选人B得到了q张选票(p>q),那么在整个点票过程中A的票数都严格大于B的概率是多少。这个问题的答案是p+qp−q
我们将此概率问题转化为一个二维格路计数 (Lattice Path Counting) 问题。
- A每得一票,路径向上走一步 (0,1)。
- B每得一票,路径向右走一步 (1,0)。
计票过程可以看作一条从原点 (0,0) 出发,经过 p+q 步到达终点 (q,p) 的路径。因为A获得 p 票(向上),B获得 q 票(向右),所以总的路径数量为:
Ntotal=(pp+q)
“A的票数始终严格领先于B”这一条件,在格路模型中意味着路径上的任意一点 (xk,yk) 均满足 yk>xk(除了起点 (0,0))。换言之,路径不能触碰或穿过对角线 y=x。
下面寻找不合规路径(“坏”路径)的策略。一条“坏”路径是指至少触碰过一次直线 y=x 的路径。所有“坏”路径可以分为两类:
- B1 类: 第一步向右(即第一张票给B)的所有路径。这样的路径在第一步就到达了 y=x下方,终点在上方,由连续性则必然穿过直线,因此所有此类路径都是“坏”路径。
- B2 类: 第一步向上(即第一张票给A),但在后续过程中至少触碰过一次直线 y=x 的路径。
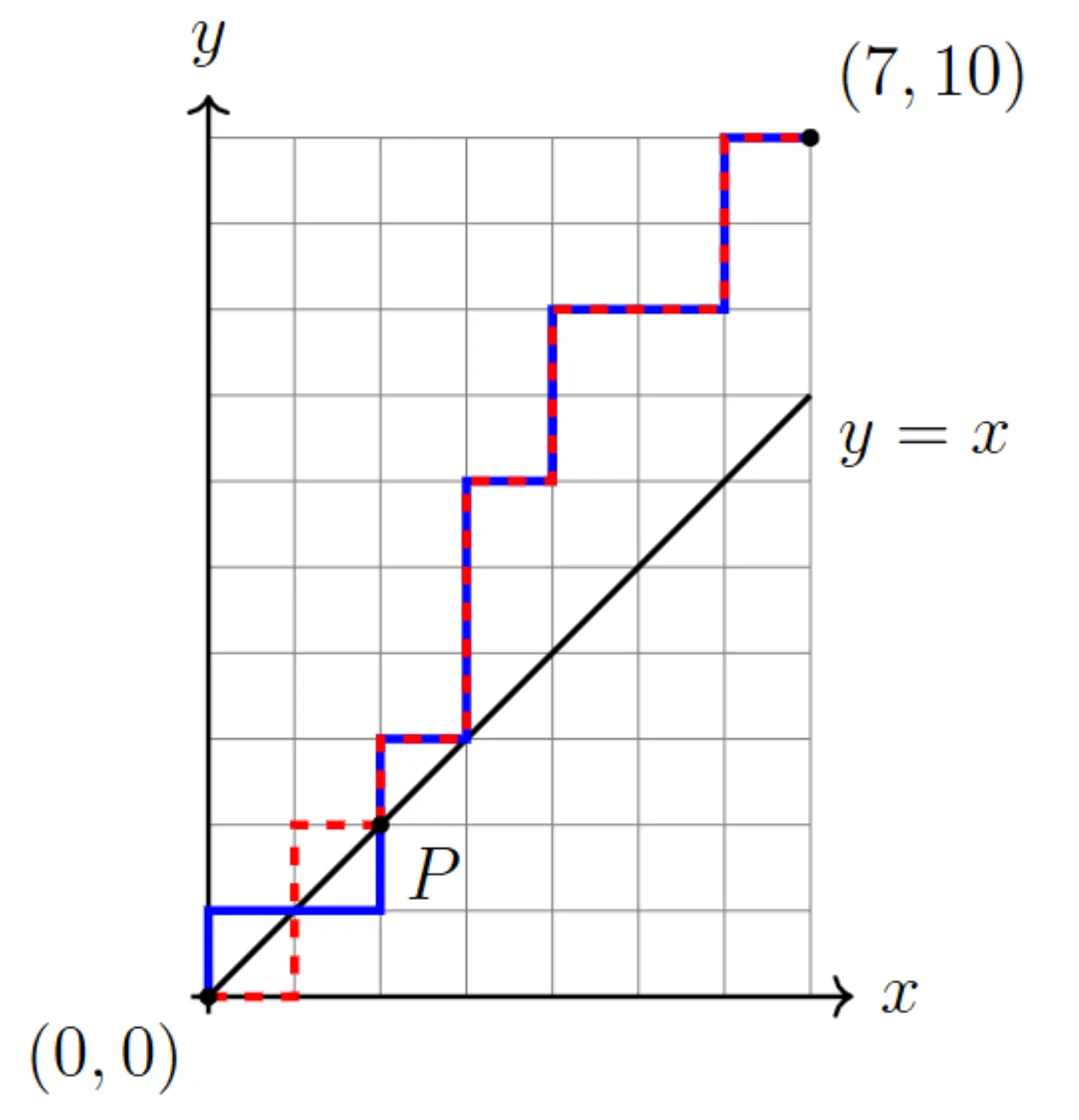
反射原理示意图,蓝色实线 ($B_2$ 类) 与红色虚线 ($B_1$ 类) 关于 $y = x$ 对称变换
从图中可以看出,对于第一步向上的情况,在路径首次触碰 y=x 的点 P 处,将触碰前的路径段关于 y=x 进行反射变换,得到一条以第一步向右开始的路径(即 B1 类路径)。这种映射是双射,因此
∣B1∣=∣B2∣=(pp+q−1)
最终的合法路径数为:
Nvalid=Ntotal−∣B1∣−∣B2∣=(pp+q)−2(pp+q−1)=p+qp−q(pp+q)
因此,A始终领先B的概率为:
P(A始终领先B)=NtotalNvalid=p+qp−q
问题中的 p0 即为 ka,从而得出上述定理。
方法二:概率母函数
- 构造指数鞅:寻找一个参数 ρ∈(0,1),使得 Zn=ρSnrn 是一个鞅。
E[Zn∣Fn−1]=E[ρSn−1+Xnrn∣Fn−1]=ρSn−1rnE[ρXn]=Zn−1rE[ρXn]=Zn−1r(21ρ1+21ρ−1)
要使其为鞅,需要 r(2ρ+ρ−1)=1,即 r=ρ+ρ−12。
-
求解参数:解方程求出 ρ=r1−1−r2 取较小的根(0<ρ<1)。
-
应用可选停止定理 :考虑停时 U=inf{n:Sn=a}。Zn 是有界鞅(0≤Sn∧U≤a),因此 E[ZU]=E[Z0]=ρS0r0=1。
E[ZU]=E[ρSUrU]=E[ρarU]=ρaE[rU]=1
因此,停时 U 的概率母函数为:
E[rU]=ρ−a=(r1−1−r2)−a
通过展开此母函数,可以得到 P(U=k) 的具体分布。
Case III:有偏随机游走(一般情况)
- 设 P(Xi=1)=p,P(Xi=−1)=q=1−p,且 p=q。
- 此时 E[Xi]=p−q=0,所以 Sn 不再是鞅。
Step 1-2: 构造鞅并计算 E[T]
- 构造补偿过程: 定义 Mn=Sn−n(p−q)。这是一个鞅,因为:
E[Mn∣Fn−1]=E[Sn−1+Xn−n(p−q)∣Fn−1]=Sn−1+E[Xn]−n(p−q)=Sn−1+(p−q)−n(p−q)=Sn−1−(n−1)(p−q)=Mn−1
- 应用可选停止定理: 对停时 T=inf{n:Sn=−a or Sn=b},应用可选停止定理于鞅 Mn。
与 Case I 类似,可证明 E[MT]=E[M0]=0。
E[ST−T(p−q)]=0⟹E[T]=p−qE[ST]
Step 3: 计算吸收概率
- 构造指数鞅:定义 Un=(pq)Sn。这是一个鞅,因为:
E[Un∣Fn−1]=E[(pq)Sn−1+XnFn−1]=(pq)Sn−1E[(pq)Xn]=Un−1(p⋅pq+q⋅qp)=Un−1(q+p)=Un−1
- 应用可选停止与收敛定理:对停时 T 应用可选停止定理于有界鞅 Un。
E[UT]=E[U0]=(pq)S0=1
展开 E[UT]:
E[(pq)ST]=(pq)−aP(ST=−a)+(pq)bP(ST=b)=1
结合 P(ST=−a)+P(ST=b)=1,解得:
P(ST=−a)=(pq)b−(pq)−a(pq)b−1,P(ST=b)=(pq)b−(pq)−a1−(pq)−a
Step 4-5: 求解 E[T] 和 E[ST]
将吸收概率代入 E[ST]=(−a)P(ST=−a)+bP(ST=b),然后可以得到 E[T]:
E[T]=p−q1(b(pq)b−(pq)−a1−(pq)−a−a(pq)b−(pq)−a(pq)b−1)
单边吸收(例如 p>q 时,游走趋向于 +∞)的情况,可以通过令 b→∞ 来分析。
二维随机游走
二维简单对称随机游走
我们考虑一个在二维整数格点 Z2 上的随机游走 Pn=(Xn,Yn),从原点 P0=(0,0) 出发。每一步,粒子等概率 (1/4) 地移动到其四个最近邻点之一,即 (±1,0) 或 (0,±1)。
令 Fn=σ(P1,…,Pn) 为自然流(包含到时刻n为止的所有路径信息)。
鞅方法及其应用
构造二维随机游走的鞅
- 坐标过程:我们定义X和Y坐标的变化Xn 和 Yn 各自都是关于 Fn 的鞅。
证明:E[Xn+1∣Fn]=E[Xn+ξn+1∣Fn]=Xn+E[ξn+1]=Xn+0=Xn。Yn 同理。
- 补偿的距离平方过程: Mn=∣Pn∣2−n=Xn2+Yn2−n 是一个鞅。
证明:E[∣Pn+1∣2−(n+1)∣Fn]=E[(Xn+ξn+1)2+(Yn+ηn+1)2−(n+1)∣Fn]=Xn2+Yn2+E[ξn+12+ηn+12]−(n+1)=∣Pn∣2+1−(n+1)=∣Pn∣2−n=Mn。这里利用了 E[ξn+12+ηn+12]=1。
- 基于离散调和函数的鞅 (最通用):若函数 f:Z2→R 是离散调和的,即满足 f(P)=41∑P′∼Pf(P′) (P’是P的邻居),则 Mn=f(Pn) 是一个鞅。
证明:E[Mn+1∣Fn]=E[f(Pn+1)∣Pn]=41∑P′∼Pnf(P′)=f(Pn)=Mn
常见的离散调和函数包括:
- f(x,y)=c (常数)
- f(x,y)=x (导出 Xn 是鞅)
- f(x,y)=y (导出 Yn 是鞅)
- f(x,y)=x2−y2 (导出 Xn2−Yn2 是鞅)
- f(x,y)=xy (导出 XnYn 是鞅)
应用一:求解撞击概率
设 D 是 Z2 上的一个有限区域,边界 ∂D=∂DA∪∂DB。粒子从 P0∈D 出发,停时 T=inf{n:Pn∈∂D}。求粒子在撞击 ∂DB 之前先撞击 ∂DA 的概率 h(P0)。
-
寻找调和函数: 寻找一个离散调和函数 h(P),满足边界条件:h(P)=1 对所有 P∈∂DA,h(P)=0 对所有 P∈∂DB。这是一个离散狄利克雷问题。
-
构造鞅: 令 Mn=h(Pn)。由于 h 是调和的,Mn 是一个鞅。
-
应用可选停止定理 (OST): 停时 T 几乎必然有限,且过程 Mn∧T=h(Pn∧T) 的值被限制在 [0,1] 内,是有界的。因此 OST 适用,E[MT]=E[M0]。
-
求解概率:
- E[M0]=h(P0)。
- E[MT]=E[h(PT)]=1⋅P(停在∂DA)+0⋅P(停在∂DB)=P(停在∂DA)。
联立得到 P(停在∂DA)=h(P0)。
结论: 撞击概率等于满足相应边界条件的离散调和函数在起始点的值。
应用二:求解期望停止时间 E[T]
问题设定同上,求解 E[T∣P0]。
鞅求解策略:
- 构造鞅:使用鞅 Mn=∣Pn∣2−n。
- 建立方程:
{E[M0]=∣P0∣2−0=∣P0∣2E[MT]=E[∣PT∣2−T]=E[∣PT∣2]−E[T]
联立得到 E[∣PT∣2]−E[T]=∣P0∣2。
结论: 求解期望时间 E[T] 的问题被转化为了求解粒子在边界上的停止位置的{\bf 期望平方距离} E[∣PT∣2]。这需要先知道粒子撞击边界各点的概率分布(即先解决撞击概率问题)。
与物理类比:离散泊松方程
求解期望停止时间 k(P)=E[T∣P0=P] 也可以通过马尔可夫链方法,建立并求解一个差分方程:
k(P)=1+41∑P′∼Pk(P′)
整理后得到离散泊松方程:
Δk(P)=−1
其中 Δk(P)=(41∑P′∼Pk(P′))−k(P) 是离散拉普拉斯算子。边界条件为 k(P)=0 对所有 P∈∂D。
这与静电学中求解有均匀电荷分布区域的电势问题相对应,而撞击概率问题则对应于求解无源区域电势的拉普拉斯方程。
附录
手写推导扫描
原稿位于文末供参考:
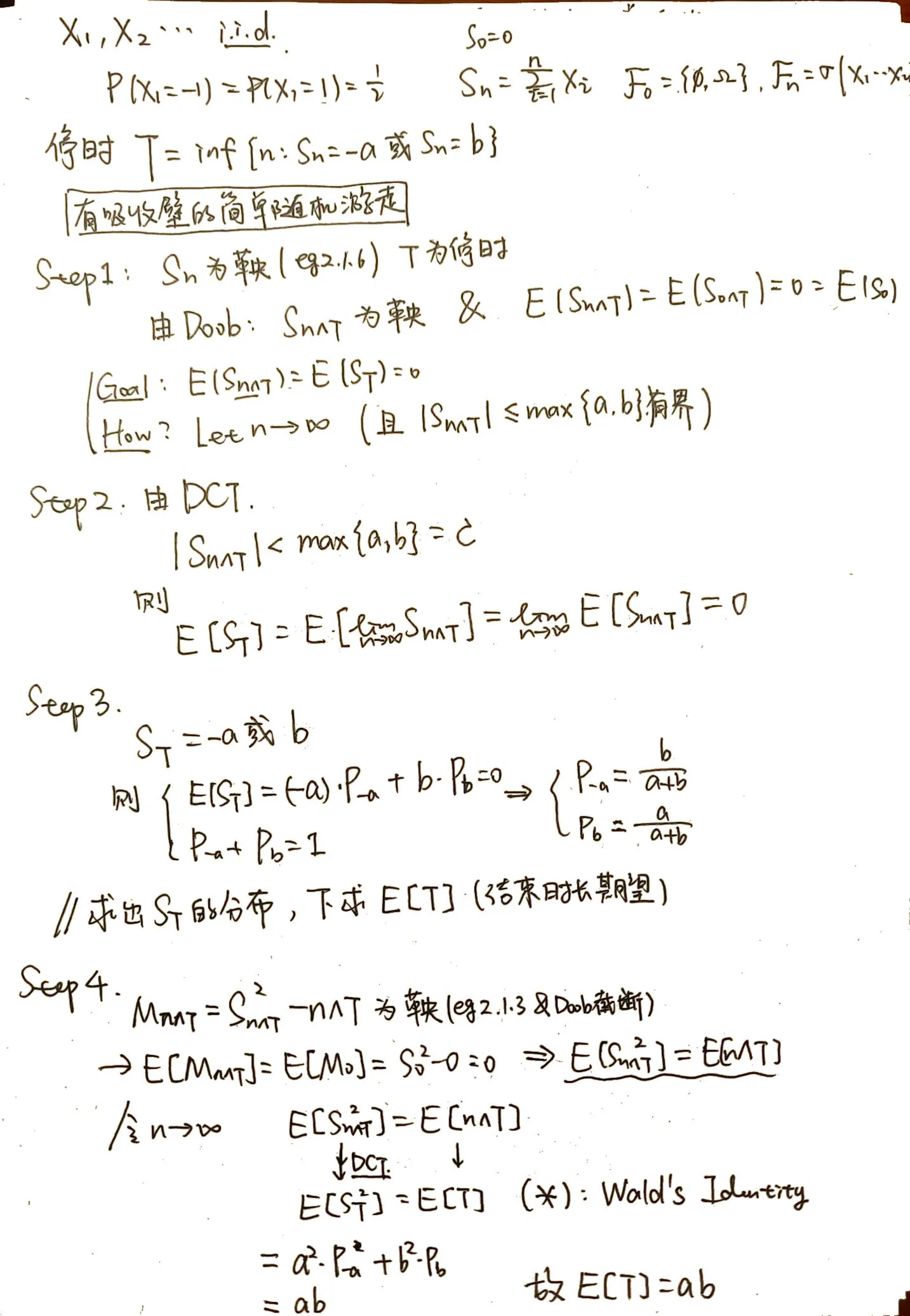




常用符号表
| 符号 | 含义 |
|---|
| Sn | 时刻 n 的游走位置 |
| Xi | 第 i 步增量,取 ±1 |
| Fn | 自然信息流 |
| T,U,Hb | 不同停时 |
| p,q | 向右/向左概率,p+q=1 |
| Mn | 构造的鞅过程 |
| E[⋅],P(⋅) | 期望与概率 |